Deskriptive Statistik
Einfach & Schnell
Inhaltverzeichnis
Die Bedeutung von deskriptiven Statistiken in der Datenanalyse
Die deskriptive Statistik dient der Beschreibung eines Datensatzes und seiner Eigenschaften. Sie nutzt Kennzahlen wie Häufigkeiten, Mittelwerte, Standardabweichungen und Grafiken, um die Verteilung und Symmetrie der Daten zu erfassen.
Wenn Sie Unterstützung bei der Erhebung oder Analyse von empirischen Daten benötigen, stehen Ihnen unsere erfahrenen Statistiker gerne zur Verfügung. Sie können unser Kontaktformular nutzen, um eine kostenlose Beratung und ein unverbindliches Angebot zu erhalten, oder uns direkt telefonisch kontaktieren. Wir helfen Ihnen dabei, Ihre Daten korrekt zu interpretieren und wichtige Erkenntnisse daraus zu gewinnen.
Die Bedeutung von deskriptiven Statistiken in der Datenanalyse
Deskriptive Statistiken spielen eine wichtige Rolle bei der Datenanalyse und sind ein grundlegender Bestandteil der deskriptiven Analyse. Die deskriptive Statistik beschreibt einen Datensatz und dessen Eigenschaften, indem sie Kennzahlen und Methoden verwendet, um eine Übersicht über die Daten zu erhalten.
Eine der wichtigsten Anwendungen von deskriptiven Statistiken besteht darin, Einblicke in die Verteilung von Daten zu gewinnen, um Trends und Muster zu erkennen. Die deskriptive Analyse kann auch zur Überprüfung von Datenqualität und zur Identifizierung von Ausreißern verwendet werden.
Um deskriptive Statistiken durchzuführen, werden verschiedene Maßzahlen wie Mittelwert, Standardabweichung, Median und Quartile verwendet. Grafiken wie Histogramme, Boxplots und Streudiagramme können auch zur Visualisierung von Daten verwendet werden.
Unsere erfahrenen Statistiker sind auf die Durchführung von deskriptiven Analysen spezialisiert und können Ihnen dabei helfen, Ihre Daten gründlich zu analysieren und zu interpretieren. Wir bieten auch Beratung und Unterstützung bei der Erhebung von Daten, um sicherzustellen, dass Ihre Daten korrekt erhoben und verarbeitet werden.
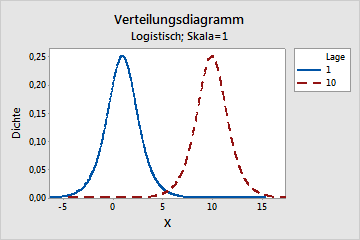

Trends und Muster erkennen: Die Rolle der deskriptiven Statistik
Die deskriptive Statistik ist ein wichtiger Bestandteil der Datenanalyse, insbesondere bei der Vorbereitung von Abschlussarbeiten wie Bachelor- oder Masterarbeiten. Eine deskriptive Auswertung kann Ihnen helfen, Ihre Daten systematisch zu analysieren und zu interpretieren, um wichtige Erkenntnisse zu gewinnen. Im Gegensatz dazu zielt die Inferenzstatistik darauf ab, allgemeine Schlüsse über eine gesamte Population auf der Grundlage von Stichproben zu ziehen.
Die deskriptive und induktive Statistik sind zwei wichtige Zweige der Statistik. Die deskriptive Statistik beschreibt und analysiert vorhandene Daten, während die induktive Statistik versucht, allgemeine Aussagen über die Population auf der Grundlage der Stichproben zu treffen.
In einer Bachelorarbeit oder Masterarbeit kann die deskriptive Statistik eine entscheidende Rolle spielen. Mit Hilfe der deskriptiven Statistik können Sie Ihre Daten gründlich analysieren und darstellen, um wichtige Erkenntnisse zu gewinnen. Unsere erfahrenen Statistiker können Ihnen dabei helfen, die richtige Methode für Ihre Arbeit zu wählen und Ihre Daten effektiv zu analysieren.
Garantien
Beste Autoren für deskriptive Datenanalyse
Eine wichtige Kennzahl zur Beschreibung von Daten ist die Verteilung, die die Breite der Streuung oder Dispersion der Werte um den Mittelwert beschreibt.
- Eine Möglichkeit, die Variationsbreite zu messen, ist der Abstand zwischen dem Minimal- und Maximalwert. Bei nominalskalierten Daten entspricht die Variationsbreite der Anzahl der Kategorien. Diese Größe hängt jedoch nur von den extremsten Werten ab und gibt keine Informationen über die Verteilung der Werte dazwische
- Quartile teilen eine Verteilung in vier gleich große Abschnitte auf und können dazu beitragen, die Verteilung besser zu verstehen. Das mittlere Quartil entspricht dabei dem Median. Die Hälfte des Abstands zwischen Q3 und Q1 wird als mittlerer Quartilabstand bezeichnet. Quartile sind besonders sinnvoll bei mindestens ordinalskalierten Werten.
- Die mittlere Abweichung beschreibt den durchschnittlichen Abstand der Werte vom Mittelwert. Bei einer symmetrischen Verteilung ergibt dieser Wert null. Es kann jedoch auch sinnvoll sein, die mittlere absolute Abweichung zu berechnen, also den Mittelwert der absoluten Abweichungen der Werte vom Mittelwert.
- Die Standardabweichung gibt an, wie weit die Werte im Durchschnitt von ihrem Mittelwert entfernt sind. Die Stichproben-Varianz wird als Mittelwert der Abweichungsquadrate berechnet, die dann durch (n-1) geteilt wird. (n steht hierbei für die Stichprobengröße.) Die Standardabweichung ergibt sich aus der Wurzel der Varianz. Die Daten sollten mindestens intervallskaliert sein, um diese Methode anwenden zu können.
- Der Variationskoeffizient teilt die Standardabweichung durch den Mittelwert. Diese Kennzahl ermöglicht den Vergleich der Streuung von Stichproben mit unterschiedlichen Mittelwerten, wenn die Werte zu einer Verhältnisskala gehören.
Zusammenfassend gibt es verschiedene deskriptive Statistiken zur Beschreibung der Verteilung von Daten. Von der Variationsbreite bis hin zum Variationskoeffizienten gibt es viele Möglichkeiten, die Charakteristiken von Daten zu messen und zu verstehen.
Jede Analyse ist möglich
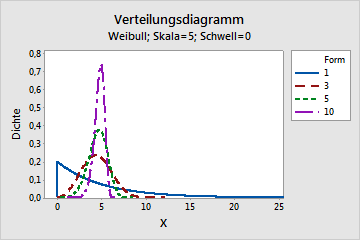
Lageparameter
Eine wichtige Größe bei der Analyse von Datensätzen sind Lageparameter, die anzeigen, ob die Werte eher groß oder klein ausgefallen sind und ob beispielsweise ältere oder jüngere Menschen befragt wurden.
- Der Mittelwert, auch arithmetisches Mittel genannt, wird berechnet, indem alle Werte aufsummiert und durch die Anzahl der Werte geteilt werden. Diese Kenngröße ist jedoch nur aussagekräftig bei Variablen, die mindestens intervallskaliert sind. Der Mittelwert kann bei kleinen Stichproben empfindlich gegenüber Ausreißern sein, da ein extrem hoher oder niedriger Wert den Mittelwert stark verändern kann.
- Der Median ist der Wert, der bei einer geordneten Reihe von Messwerten genauso viele Werte darüber wie darunter hat. Bei einer ungeraden Anzahl von Werten ist es genau der mittlere. Diese Größe ist aussagekräftig bei Variablen, die mindestens ordinalskaliert sind.
- Der Modalwert oder Modus ist der Wert in einer Verteilung, der am häufigsten auftritt. Wenn die Werte zu Klassen zusammengefasst werden, gilt die Klassenmitte der häufigsten Klasse als Modalwert der Verteilung. Diese Größe kann für alle Skalenniveaus verwendet werden, auch für eine Nominalskala. Der Modalwert ist robust gegenüber Ausreißern und eignet sich besonders gut, um die Häufigkeiten von Werten zu analysieren.



